Rob Siegwart - Failure Theories

For part stresses that are multi-axial, failure theories relate the failure in a part subjected to arbitrary multi-axial loads to that of a uni-axially loaded test specimen. The general form of these relationships are:

\begin{equation*} M_{part}\geq M_{specimen} \end{equation*}

Where M is a “modulus” chosen by each theory that can be either calculated or measured in the part and test specimen, and then compared to assess failure. Often the modulus is a function of the principal normal or shear stresses.

\begin{equation*} f(\sigma_1,\sigma_2,\sigma_3)\geq \sigma_c \end{equation*}

\begin{equation*} f(\tau_1,\tau_2,\tau_3)\geq \tau_c \end{equation*}

where \(\sigma_c\) and \(\tau_c\) are the chosen characteristic failure strengths from the uniaxial tension test.

The major theories are:

Maximum Normal Stress Theory

Failure (i.e. yielding, fracture) is expected to occur if the maximum normal stress in the part exceeds the maximum normal stress in test specimen at failure (yielding, fracture).

\begin{equation*} \max(\sigma_1,\sigma_2, \sigma_3)\geq \sigma_c \end{equation*}

\begin{equation*} \min(\sigma_1,\sigma_2,\sigma_3) \leq \sigma_c \end{equation*}

where \(\sigma_t\) and \(\sigma_c\) are test specimen tensile and compressive strengths, respectively.

This theory is applicable to brittle materials but not to ductile materials.

Maximum Shearing Stress Theory

Here failure is predicted to occur if the maximum shearing stress (the principal shearing stress) is equal to or exceeds the maximum shear stress in a test specimen at failure.

\begin{equation*} \max(|\tau_1|, |\tau_2|, |\tau_3|) \geq \tau_c \end{equation*}

\(\tau_c\) is the maximum shearing stress in the test specimen, and for a uniaxial tension test the max shear stress occurs at 45 degrees to the applied load direction and is equal to half of the first principal stress, which is the nominal tensile stress.

This theory applies well to ductile materials and to ductile yielding.

Distortion Energy Theory (von Mises)

This theory postulates that the distortion energy - that which contributes to shape change and not to change in volume - affects the failure of the part. Dilation energy, that which only changes the volume, does not contribute to the failure of the part. The latter is produced by hydrostatic stress, which has been shown to not induce yielding or fracture (none under compression, but fracture under high levels of tensile stress).

The equation for the distortion energy theorem is:

\begin{equation*} \frac{(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2}{2} \geq \sigma_f^2 \end{equation*}

The left side of the equation when (sigma_f) is solved is the von Mises stress:

\begin{equation*} \sigma_{vm} = \sqrt{\frac{(\sigma_1-\sigma_2)^2 + (\sigma_2-\sigma_3)^2 + (\sigma_3-\sigma_1)^2}{2}} \end{equation*}

The yield and failure surface can be plotted, obtaining an infinite cylinder. According to the theory all stress points that lie within the surface do not produce failure and those outside do.

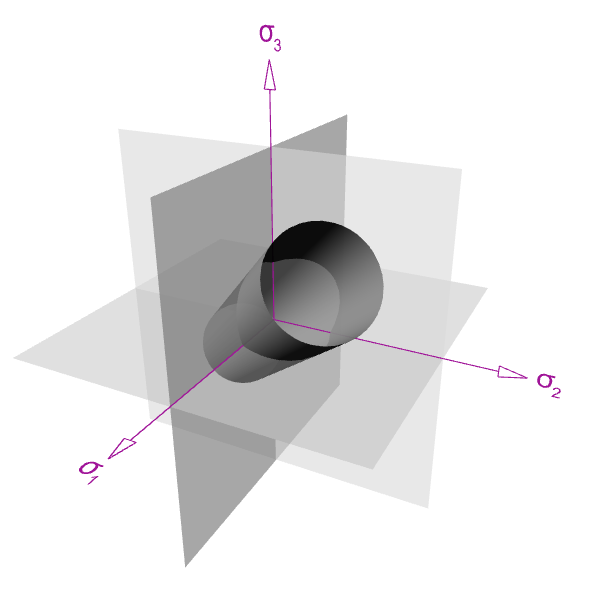
Von mises yield surface plot in 3 dimensions

For a 2D stress state, the yield surface produces an elliptical failure curve when intersected with a plane.

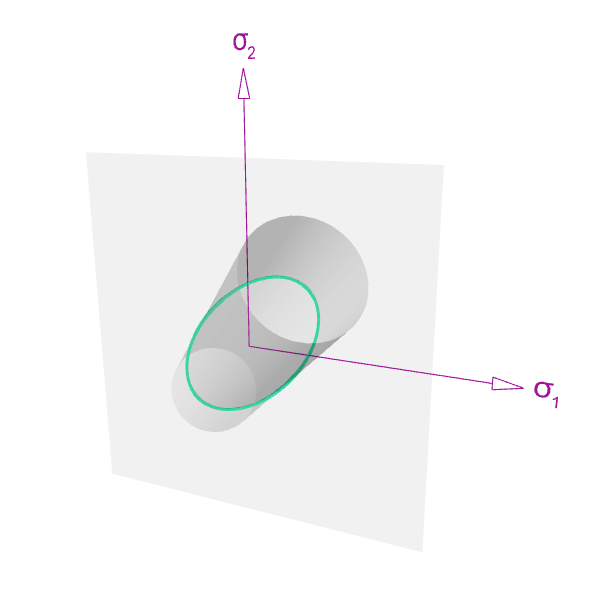
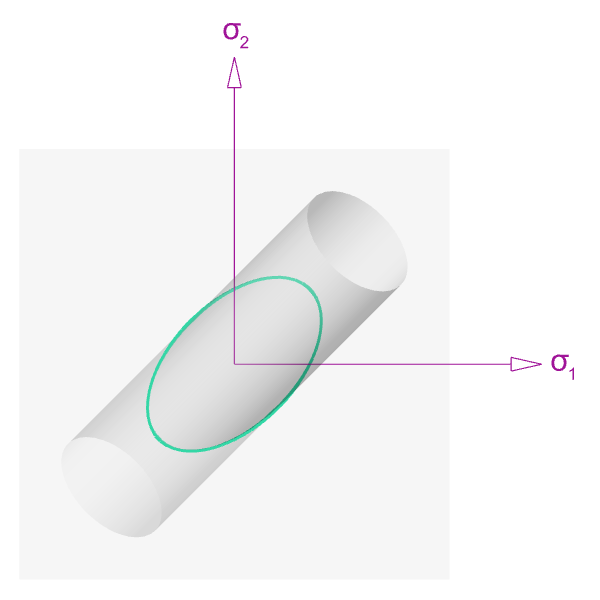
Von mises yield surface plot in 2 dimensions with elliptical intersection with sigma1-sigma2 plane

This can be verified by setting \(\sigma_3\) equal to 0 and plotting. With a constant of 1:

Von mises yield surface plot in 2 dimensions